第3回では、2つの銘柄を保有することでリスクが低下するということを説明しました。今回は、さらに複数、つまり3つ以上の異なる銘柄を保有するときのリスクとリターンについて考えてみましょう。一般的には、3つ以上の異なる銘柄を組み合わせた投資は、2つだけを組み合わせた投資よりもリスクを低減できる可能性があります。それぞれの銘柄の保有割合を変えてみると、リスクが大きく変化するのです。このようにしてリスクを調整しながらリターンが最大になる点を線でつないだものを「効率的フロンティア」と言います。この効率的フロンティアは、同じリスクで得られる最大のリターンを示しています。
1. 2銘柄ポートフォリオのリスクとリターン
まずは前回、第3回で学んだ、2つの株式を組み合わせたポートフォリオのリスクとリターンについて振り返りましょう。図1は、A社とB社の株式それぞれのリスクとリターンを示したグラフです。ここで、横軸はリスクを、縦軸はリターンを表しています。この図1を見ると、A社の株式はB社に比べて、リスクもリターンも大きいことがわかります。
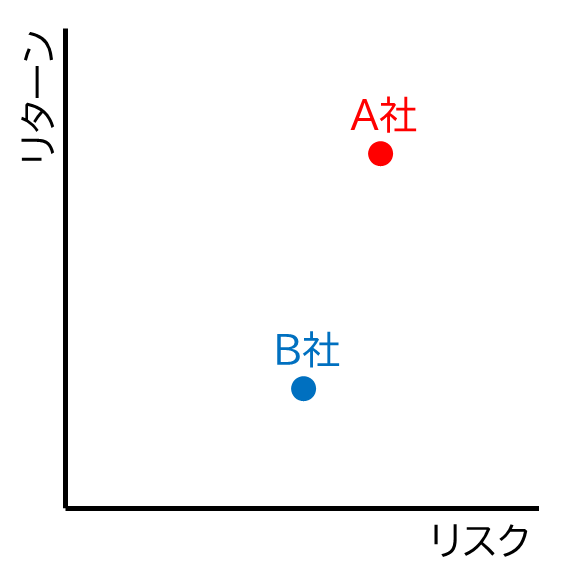
第3回の内容を思い出すと、A社とB社の株式を適切に組み合わせることで、全体のリスクを低減することが可能でした。例えば、A社とB社の株式を均等に、つまり各50%ずつ購入すると考えてみましょう。具体的には、1万円の投資資金を使って、A社とB社の株式をそれぞれ5,000円ずつ購入するといった具合です。すると、リスクは図2に示されるように減少することが期待できるのです。

もちろん、A社とB社の株式を必ずしも均等に購入するという決まりはありません。どのくらいの比率で購入するかは、自由に決めることができます。例えば、A社の株式を全体の75%、B社の株式を全体の25%購入するという組み合わせも可能です。また、その逆で、A社を25%、B社を75%購入するという組み合わせも考えられます。このように、A社とB社の株式の購入比率を少しずつ変化させてみると、リターンとリスクの関係を表す曲線が図3のように描かれます。このリスクとリターンの具体的な計算方法については、記事の最後に説明しています。

さらに、第3回の内容で、リスクが必ずしも減少しないケースも学んだことを覚えていますか?それは、A社とB社の株価が同じ方向に動くときです。リスクとリターンの関係を図で表すと、それは図4のように直線的になります(専門用語で言うと、これはA社とB社の株価の相関係数が1である状態を示しています)。このケースでは、リスクとリターンは直線で結ばれますが、リスクが大きく減少するということはありません。

2. 3銘柄ポートフォリオ
3つの銘柄を組み合わせて投資する場合でも、リスクとリターンの関係を計算することは可能です。ただし、3つの銘柄を組み合わせると、その比率が複雑に変わるため、リスクとリターンの関係は図3や図4のような線ではなく、図5の緑色で示された範囲のようになります。一般的には、3つ以上の銘柄を組み合わせた場合でも、リターンは各銘柄の保有割合による加重平均となり、リスクは低減する傾向にあります。
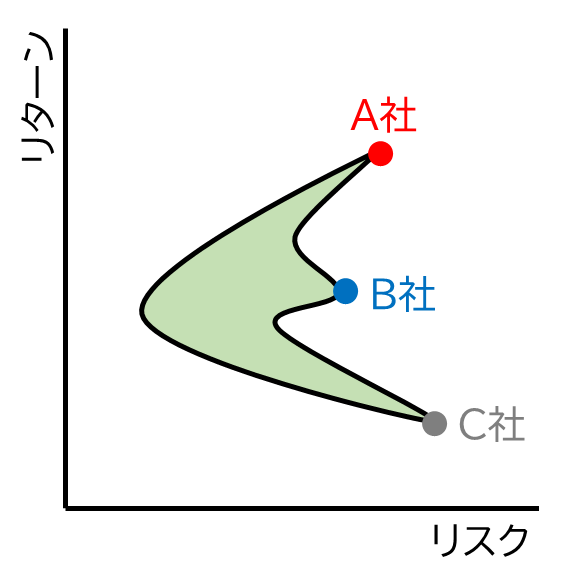
3. 効率的フロンティア
ここまでで、多様な株式を組み合わせる分散投資を行うと、リスクを抑えられることを示しました。しかし、投資を行うにあたり、最適な株式の組み合わせはどのようにして選び出せば良いでしょうか?一つの考え方として、リスクをある一定の値に設定し、その条件下でリターンが最大となる組み合わせ銘柄を選ぶという方法があります。図6では、リスクをRと設定した場合に得られるリターンの範囲を示しています。
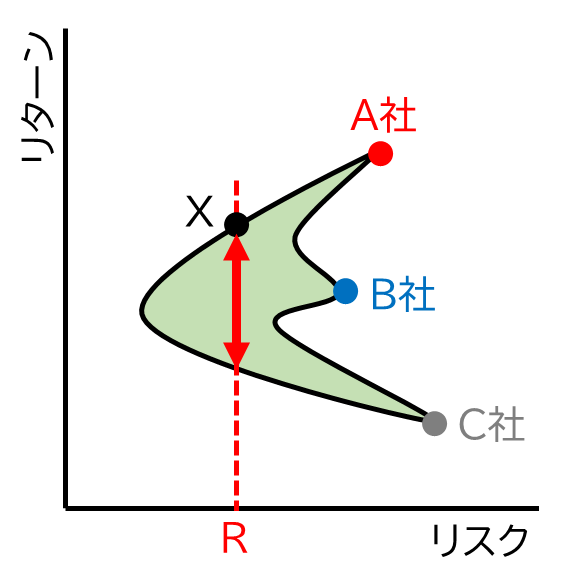
この図を見てみると、同じリスクレベルRで投資をする場合、リターンは高いほうが良いということなので、X点が選ばれることでしょう。なぜなら、X点よりも下の緑の範囲にある点を選ぶと、リスクは同じでもリターンが低くなってしまうからです。この考え方を一般化すれば、投資家は図7の緑の線上の点を選ぶべきだという結論に至ります。なぜなら、リスクがRaからRbの範囲であるときに、緑の線上が最大のリターンをもたらすからです。この緑の線を「効率的フロンティア」と呼んでいます。
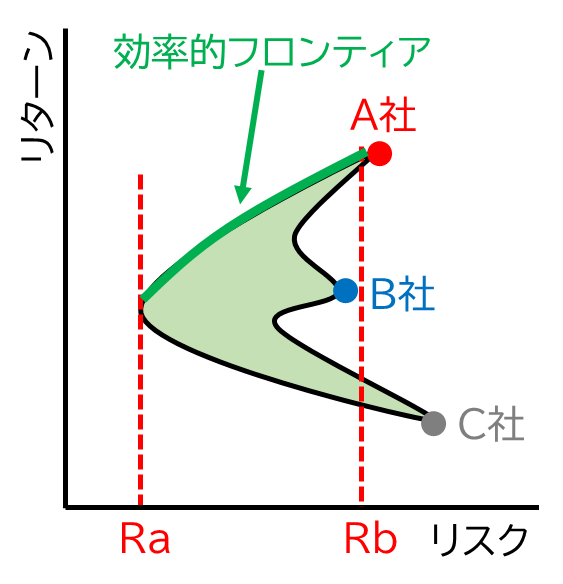

4.リターンとリスクの計算方法(参考)
これから先の参考は、数式を使った説明となり、少々難易度が上がります。銘柄の組み合わせによってどのようにリスクを低減できるのか、具体的な計算方法を示します。特に興味がある方だけお読みいただければと思います。
2銘柄の場合のリターンとリスク
表1のようにA社とB社のリターン\(μ_{A}\)と\(μ_{B}\)、A社とB社のリスク\(σ_{A}\)と\(σ_{B}\)、A社とB社の組み入れ比率\(w_{A}\)と\(w_{B}\)、A社とB社の相関係数を\(ρ_{AB}\)と定義します。\(ρ_{AB}\)は第3回で勉強したように株価が同じように動く(正の相関)か逆に動くか(負の相関)を示すものです。
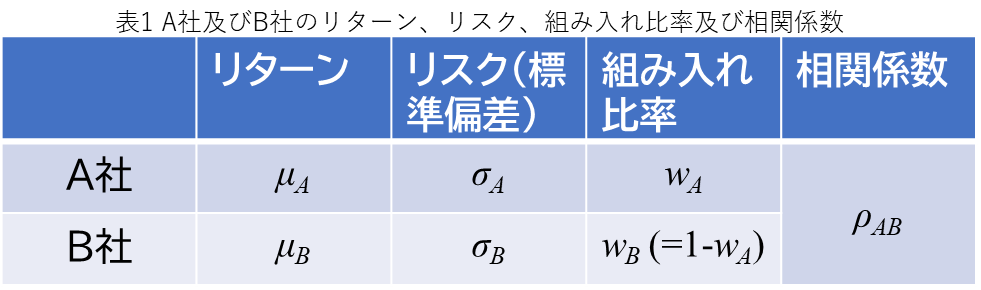
このとき、組み合わせ、つまりポートフォリオのリターン\(μ_{p}\)は
\begin{eqnarray}
μ_{P} =w_{A}μ_{A}+w_{B}μ_{B}
\end{eqnarray}
となります。リターンは加重平均で表すことできます。一方、ポートフォリオのリスク\(σ_{p}\)は
\begin{eqnarray}
σ_{P} =\sqrt{w_{A}^{2}σ_{A}^{2}+w_{B}^{2}σ_{B}^{2}+2ρ_{AB}w_{A}w_{b}σ_{A}σ_{B}}
\end{eqnarray}
例えば、\(μ_{A}=7\)%と\(μ_{B}=9\)%、A社とB社のリスク\(σ_{A}=15\)%と\(σ_{B}=20\)%、A社とB社の組み入れ比率\(w_{A}=0.4\)と\(w_{B}=0.6\)、A社とB社の相関係数を\(ρ_{AB}=0\)とするとリターン\(μ_{P}\)とリスク\(σ_{P}\)は以下のようになります。
\begin{align*}
&μ_{P} =0.4×0.07+0.6×0.09=0.082\\
&σ_{P} =\sqrt{0.4^2×0.15^2+0.6^2×0.2^2+2×0×0.4×0.15×0.6×0.2}=0.12
\end{align*}
よって、\(μ_{P}\)=8.2%、\(σ_{P}\)=12%になります。この計算から2つの銘柄を組み合わせることによって、リターンは加重平均となり、リスクは大幅に低下させることができます。なお、上記を計算の際は%は一旦外して0.01を掛けから計算する必要があることに注意して下さい。
3銘柄の場合のリターンとリスク
表1のようにA社、B社及びC社のリターン\(μ_{A}\)、\(μ_{B}\)及び\(μ_{C}\)、A社、B社及びC社のリスク\(σ_{A}\)、\(σ_{B}\)及び\(σ_{C}\)、A社、B社及びの組み入れ比率\(w_{A}\)、\(w_{B}\)及び\(w_{C}\)、A社とB社、B社とC社及びC社とA社の相関係数を\(ρ_{AB}\)、\(ρ_{BC}\)及び\(ρ_{CA}\)と定義します。

このとき、組み合わせ、つまりポートフォリオのリターン\(μ_{p}\)は
\begin{eqnarray}
μ_{P} =w_{A}μ_{A}+w_{B}μ_{B}+w_{C}μ_{C}
\end{eqnarray}
となります。リターンは加重平均で表すことできます。一方、ポートフォリオのリスク\(σ_{p}\)は
\begin{eqnarray}
σ_{P} =\sqrt{w_{A}^{2}σ_{A}^{2}+w_{B}^{2}σ_{B}^{2}+w_{C}^{2}σ_{C}^{2}+2ρ_{AB}w_{A}w_{B}σ_{A}σ_{B}+2ρ_{BC}w_{B}w_{C}σ_{B}σ_{C}+2ρ_{CA}w_{C}w_{A}σ_{C}σ_{A}}
\end{eqnarray}
となります。
\(N\)銘柄の場合のリターンとリスク
\(N\)銘柄ある場合のポートフォリオのリターン\(μ_{p}\)とポートフォリオのリスク\(σ_{p}\)は
\begin{eqnarray}
μ_{P} =\sum_{n=1}^N w_{n}μ_{n}
\end{eqnarray}
\begin{eqnarray}
σ_{P} =\sqrt{\sum_{m=1}^{N} \sum_{n=1}^{N} σ_{mn}w_{m}w_{n}}
\end{eqnarray}
ここで、\(σ_{mn}\)は\(m\)社と\(n\)社の価格変動の共分散を示します。














