プロペクト理論とは
プロスペクト理論(Prospect Theory)は、経済学や心理学の分野で用いられる決定理論の一つで、特にリスクを伴う状況下での人間の判断や選択を説明するために開発されました。この理論は、ダニエル・カーネマンとアモス・トベルスキーによって1979年に提唱され、彼らの研究は行動経済学の分野に大きな影響を与えました。
プロスペクト理論は、人間の判断が常に合理的ではなく、様々な認知バイアスや心理的要因の影響を受けることを示唆しています。この理論は、金融市場、保険、マーケティング、政策立案など、多くの分野で応用されています。
プロスペクト理論の例
次のA株,B株が50万円で売っているとして、どちらを買うか考えてみてください。
- A株 : 50%確率で増えないが、50%の確率で100万円になる。
- B株 : 確実に75万円になる。
儲けの期待値はどちらも25万円ですが、ほとんどの人はB株を選択します。
別な例を見てみます。あなたは損しそうなC株、D株を持たなければならないとします。どちらか選択しろと言われたらどちらを選択しますか?
- C株 : 50%の確率で50万円損するが、50%の確率で損はゼロにできる。
- D株 : 確実に25万円損する。
どちらも損の期待値は25万円ですが、ほとんどの人はC株を選択します。
人はポジティブな場合は確実性のあるものを選択します(B株を選ぶ)。逆にネガティブな場合はリスクを何の損ものないものに賭けようとします(C株を選ぶ)。利益が得られるような局面では確実に利益を取ることを好み、逆に損しそうな局面ではギャンブルすることを好むのです。
効用曲線
これをモデル化したものが効用曲線です。原点を右に行くか(儲かるとき)、左に行くか(損するとき)で人の判断が異なってくるという面白い結果になります。それについて次から詳しく説明していきます。
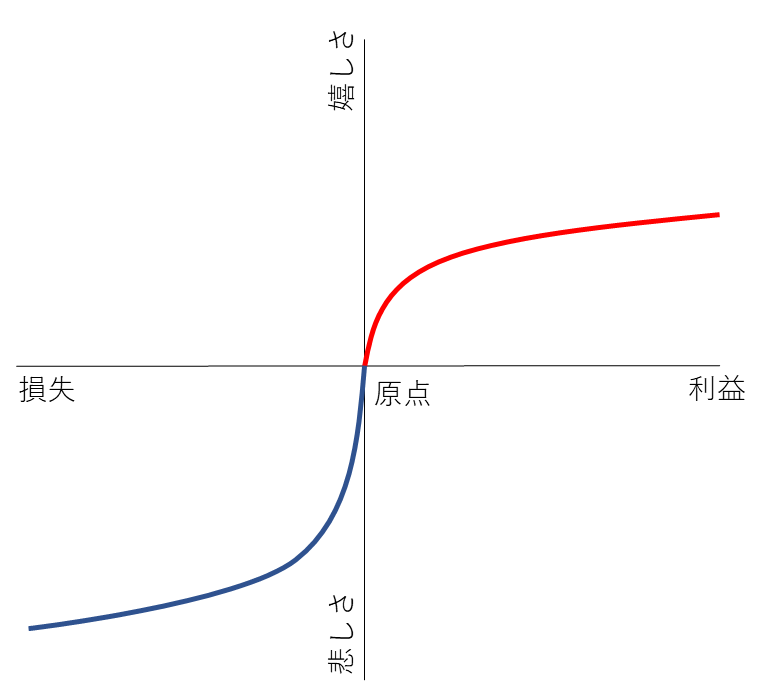
儲けるとき(図1の原点より右側の赤線)
株式投資において、人は利益が出ると早く利確したくなります。それは上記のB株を選択するようなものです。確実に儲けたいのです。
また、儲かれば儲かるほど人が感じる嬉しさは減っていく傾向にあります(限界効用)。

ある程度儲けるとそれ以上儲けても嬉しさはあまり増えないのです。例えば、株を買ってすぐに1万円増えるととても嬉しいでしょう。

しかし、どんどん増えていって、100万円から101万円増えてもそれほど嬉しくないでしょう。増える額は同じ1万円なのにです。

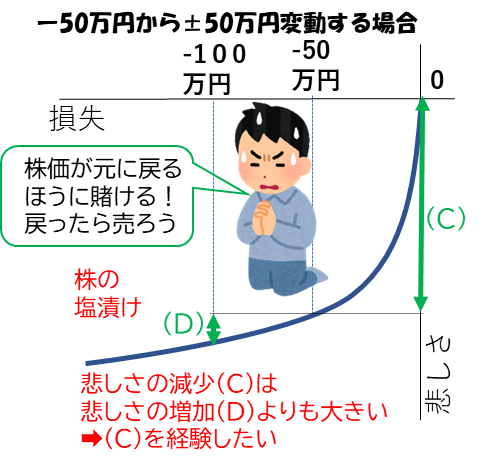
しかもやっかいなことに、人は増えたものが減ってしまう損に対しては敏感でです。例えば、現在の儲けが50万円だったとしましょう。ここから(A)50%の確率でさらに50万円上がる、(B)50%の確率で50万円下がる、の2つの可能性があれば、人は利確を急ぐ傾向があります。それは増加する嬉しさよりも価格が下がることによる嬉しさの減少が大きいからです。
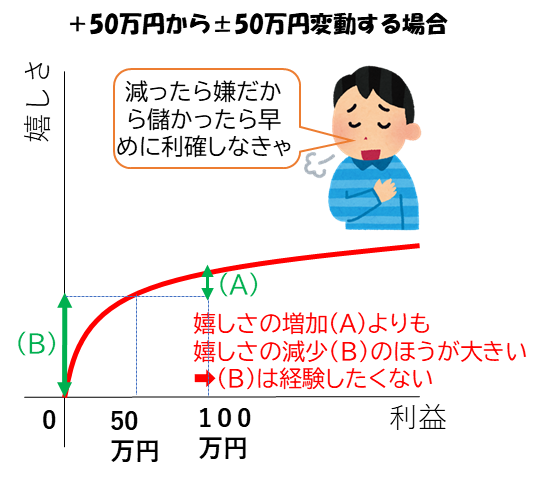
人には、減る恐怖が増える嬉しさを上回る傾向があり、この性質は株式投資において同じ株をずっと持ち続けるのを難しくさせています。
損するとき(図1の原点より左側の青線)
人はちょっとした損失でも痛みは大きいものです。もう一度、図1を見て欲しいのですが、プラスの赤線よりもマイナスの青線のほうが大きく、悲しさの振れが大きいことが分かります。人は儲ける嬉しさよりも損するダメージのほうが大きいのです。
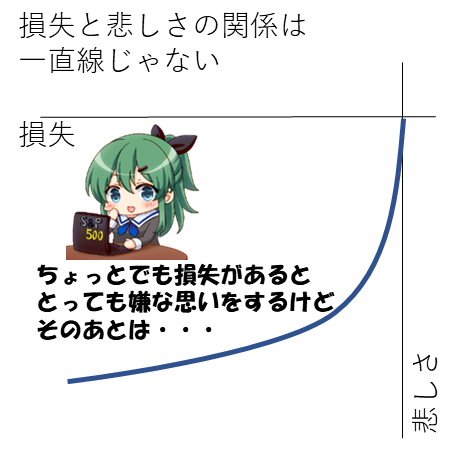
それゆえ、ちょっとの損でも株を手放してしまうこともよくあります。
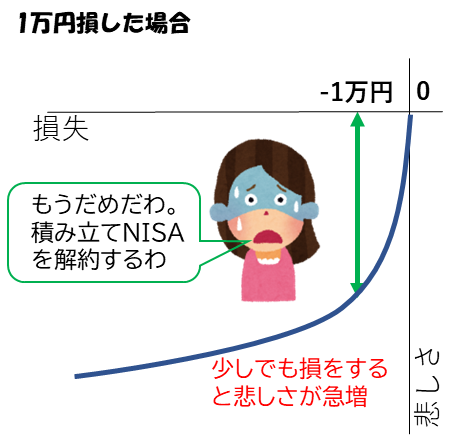
しかし、大損している場合はそれ以上損してもあまり痛みは増加しません。そのため、人は損切りを躊躇します。
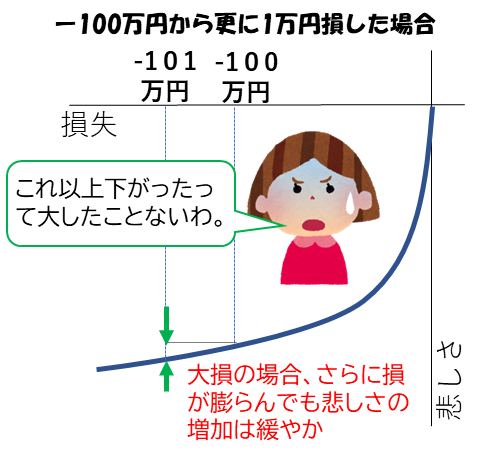
このことから図9のことが言えます。損が回復する悲しさの減少は損拡大の悲しさの増加よりも大きいのです。これが含み損の株が塩漬けになる原因となります。また、人は上述のC株を選択するよう、損を確定させたくありません。だから、含み損の株は売ることができないのです。
結論
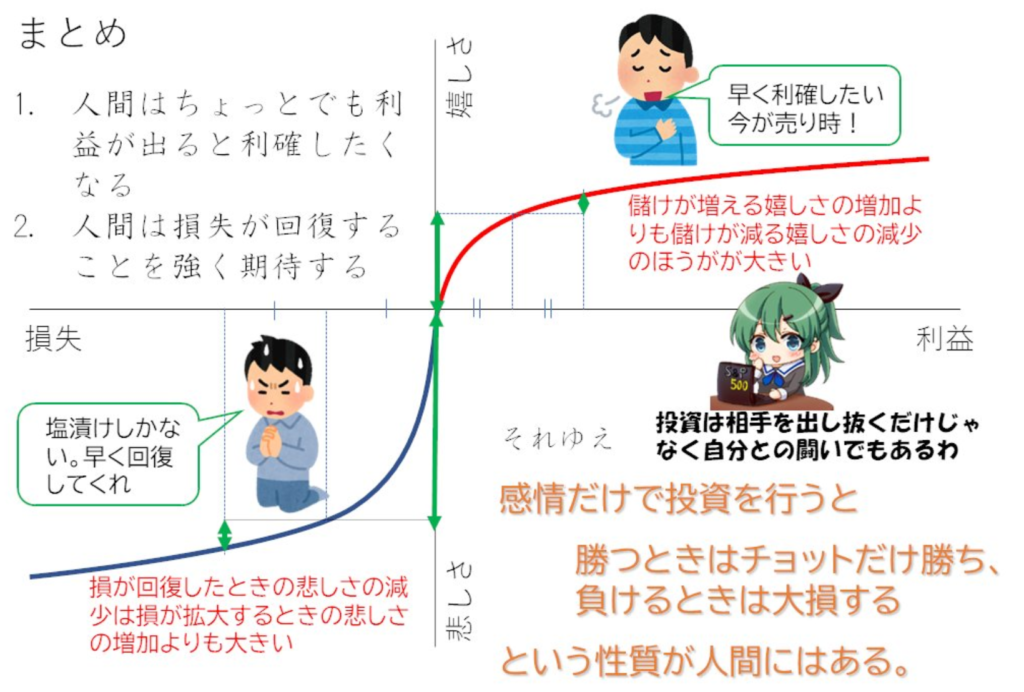
まとめ。プロスペクト理論によれば
- 人は株で儲ければすぐに利確したい。
- 人は株で損すれば元に戻ることを期待する 。
それゆえ、 『人は儲けるときは少額だけ儲け、損するときは大金を失う。』という事態が発生しやすいのです。 株は自己との闘いでもあるということはプロスペクト理論からも納得できるでしょう。
【参考文献】田渕直也, ”ファイナンス理論全史,” ダイヤモンド社、2017年12月.









